Введение в системы управления базами данных
Рассмотрим более сложное отношение эквивалентности.
Пример 2
. Рассмотрим более сложное отношение эквивалентности. На множестве целых чисел
и 
равны по модулю n, если их остатки при делении на n равны. Например, по модулю 5 равны числа 2, 7, 12 и т.д.
Условия 1-3 легко проверяются, поэтому равенство по модулю является отношением эквивалентности. Предикат этого отношения имеет вид:
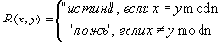Классы эквивалентности этого отношения состоят из чисел, дающих при делении на n одинаковые остатки. Таких классов ровно n:
[0] = {0, n, 2n, …}
[1] = {1, n+1, 2n+1, …}[n-1] = {n-1, n+n-1, 2n+n-1, …}
