Введение в системы управления базами данных
Теорема (Фейджина)
Теорема (Фейджина)
. Пусть
, 
.
Декомпозиция отношения 
и 
.
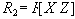
Замечание. Если зависимость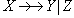 
или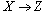 
Доказательство теоремы.
Необходимость. Пусть декомпозиция отношения 
и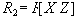 
.
Предположим, что отношение 
и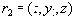 
также содержится в 
содержится в 
содержится в 
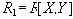
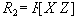
содержится в естественном соединении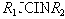 
. Необходимость доказана.
Достаточность. Пусть имеется многозначная зависимость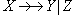 
на проекции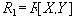 
является декомпозицией без потерь.
Как и в доказательстве теоремы Хеза, нужно доказать, что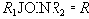 
.
Включение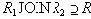 
.
Докажем включение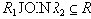 
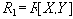
. Это означает, что в проекции 
, а в проекции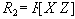 
. По определению проекции, найдется такое значение 
, что отношение 
. Аналогично, найдется такое значение 
, что отношение 
. Тогда по определению многозначной зависимости кортеж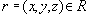 
Достаточность доказана.
